Sigma Clipping in Random Vibration Tests Explained
In conventional random test, the output random signal satisfies Gaussian distribution, signal peaks greater than 3 sigma occupy less time. Therefore, we generally take 3sigma as the upper limit of the calculation in actual calculations.
During the random vibration test, the peak signal greater than 3sigma may cause the input of the power amplifier to be too high and cause an alarm. So you can cut off the peak signal greater than 3sigma to ensure that the voltage input of the amplifier during the high level test, to ensure the output power of the power amplifier.
PART 1 - 3 Sigma Principle
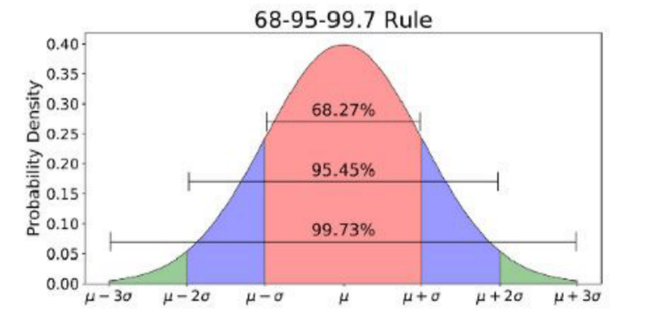
Generally, the output random signal satisfies Gaussian distribution in conventional Random test. The Gaussian distribution is the distribution characteristic of the random vibration signal in the amplitude domain. As show in Figure 1.
Figure 1
In the Gaussian distribution, σ is the standard deviation, and μ is the average value.
There is a 3 sigma principle for random signals with Gaussian distribution. The 3 sigma principle is:
The probability that the value is distributed in (μ-σ, μ+σ) is 68.27%;
The probability that the value is distributed in (μ-2σ, μ+2σ) is 95.45%;
The probability that the value is distributed in (μ-3σ, μ+3σ) is 99.73%;
In the random test, the average value is 0, the standard deviation is the effective value, so the above principle can also be described as:
68.27% of the values are distributed within 1 times the effective value;
95.45% of the values are distributed within 2 times the effective value;
99.73% of the values are distributed within 3 times the effective value
According the above values, the probability of exceeding 3 times the effective value is about 0.3%.
According to the distribution law of normal random signals, there will be 3 points out of the range of 3 times the effective value for every 1000 points. There will be 7-8 points per second that exceed 3 times the effective value.
PART 2 - Sigma Clipping Application
In the fields of engineering technology such as aerospace, electronics and electrical components, many environmental vibrations are random vibrations. Due to the high level of some random test, sigma clipping is often required. For example, the effective value of acceleration in test condition K is 47.23g (GJB360B-2009 standard test, in table 214-1 )
The test was run twice in the random module. The following figure shows the time-domain recording signal when sigma clipping is disabled and iterative 3 sigma.
Disable:
Figure 2
Iteration:
Figure 3
By comparison, we can found that the probability of the peak signal exceeding ±3sigma is significantly reduced.
PART 3 - Sigma Clipping Feature
The VENZO 880 software includes two sigma clipping options: "regular" and "iterative". “Regular” performs digital clipping of the driving voltage signal. The advantages of this method are simplicity and small amount of calculation. The disadvantage is that the waveform distortion is large, the dynamic range of the control spectrum is significantly reduced, and the peak factor of the response signal is not significantly reduced.
We have add an "iterative" option in the sigma clipping. The "iterative" method is based on time-domain clipping and frequency-domain phase adjustment algorithms. Compared with conventional sigma clipping, iterative sigma clipping has two major advantages: better clipping effect and greater control dynamic range.
Better Clipping Effect
Through iterative sigma clipping, the random test with the larger effective value can be made to ensure that no excessive drive peak signal input the shaker system during the operation. For example, the effective value of acceleration in test condition K is 54.855g (GJB360B-2009 standard test, Table 214-2 ), as shown in figure 4.
Figure 4
Using iterative 3sigma, the acceleration time-domain recording signal is shown in figure 5. It can be seen that the peak value is 180.98g in the time domain , which is approximately 3.3 times the effective value. As shown in Figure 5.
Figure 5
If you use conventional 3sigma clipping, the time-domain recording signal of acceleration is shown in figure 6. It can be seen that the peak value is 224.97g in the time-domain, which is approximately 4.1 times the effective value.
Figure 6
It can be seen that the iterative sigma clipping has the better clipping effect, which can better ensure the safety and reliability of the test.
Larger dynamic range of control
Using iterative sigma clipping can ensure that when the sigma clipping coefficient is greater than 2.8, the dynamic range of the control spectrum is not affected at all. Using iterative 3sigma clipping, the 90dB random spectrogram is shown in figure 7, and the dynamic range of control can reach 90dB.
Figure 7
Using regular 3sigma clipping, the control effect of 90dB random spectrogram is shown in the figure 8, and the control dynamic range is about 40dB.
Figure 8
It can be seen that the control dynamic range of iterative sigma clipping is higher, which can better meet the needs of sigma clipping in random test with the large dynamic range.